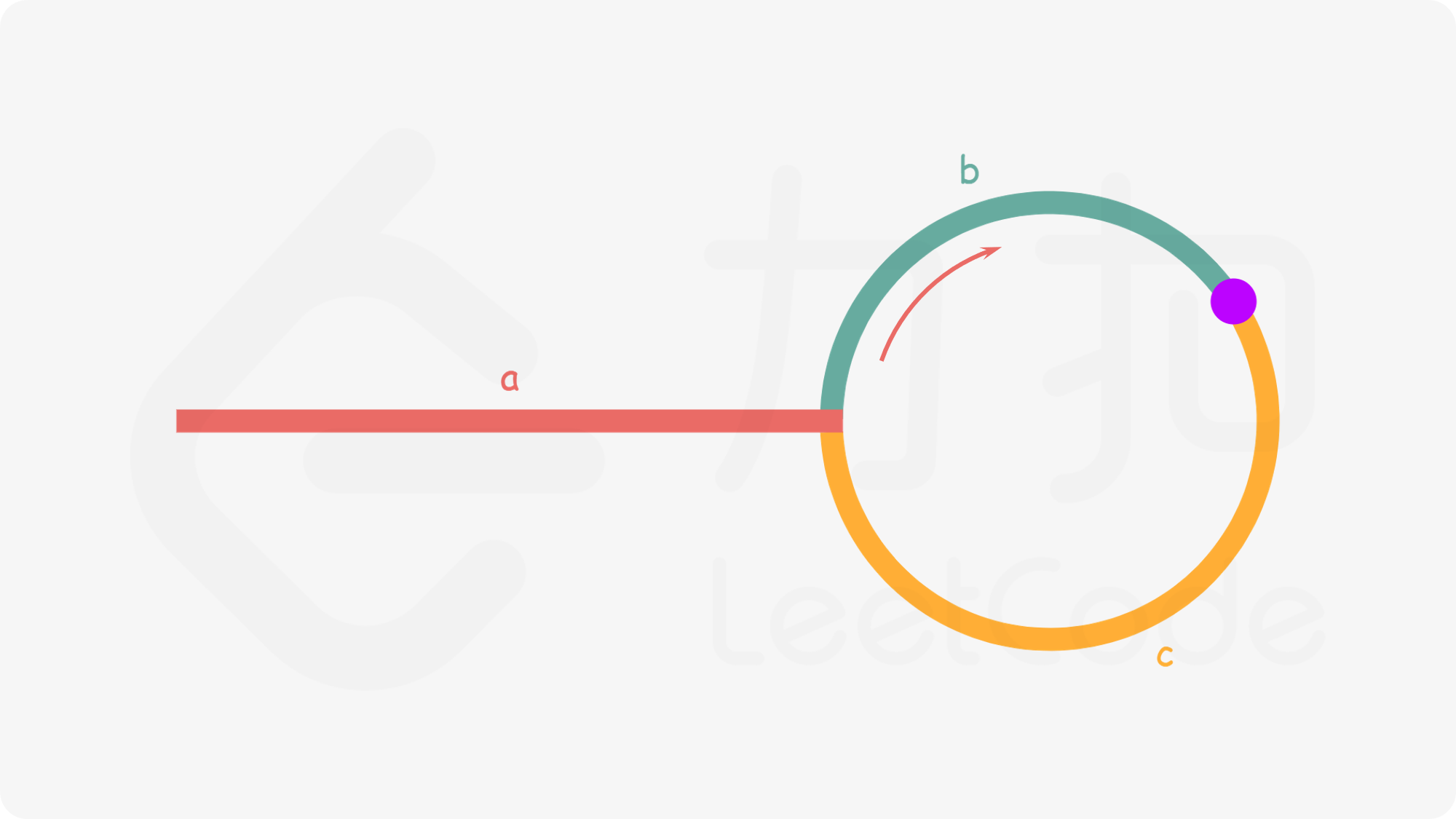002_链表 - Leetcode - 编程

# 一、理论基础

也没什么特别的。离散存储、不支持随机访问。

链表节点的定义：

template <class T>
struct _listNode {
    void* m_prev;
    void* m_next;
    T m_data;
    _listNode(T x) : m_data(x), m_next(nullptr), m_prev(nullptr) {}
};

# 二、题目实践

# 1、203. 移除链表元素

添加一个头节点，然后一次遍历即可。除了要释放我们移除的节点外，最后还要记得释放 dummy 节点：

class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) {
        ListNode* pDummy = new ListNode(-1, head);
        ListNode* pNow = pDummy;
        while(pNow->next != NULL) {
            if(pNow->next->val == val) {
                ListNode* pDel = pNow->next;
                pNow->next = pDel->next;
                delete pDel;
            } else {
                pNow = pNow->next;
            }
        } head = pDummy->next;
        delete pDummy;
        return head;
    }
};

# 2、707. 设计链表

struct MyNode {
    int val = 0;
    MyNode* next = nullptr;
    MyNode() : val(0), next(nullptr) {}
    MyNode(int x) : val(x), next(nullptr) {}
    MyNode(int x, MyNode* p) : val(x), next(p) {}
};

class MyLinkedList {
public:
    MyLinkedList() : m_length(0) {
        m_head = new MyNode(-1, nullptr);
    }
    
    int get(int index) {
        if(index >= m_length) { return -1; };
        MyNode* pNow = m_head->next;
        while(index--) {
            pNow = pNow->next;
        } return pNow->val;
    }
    
    void addAtHead(int val) {
        MyNode* pAdd = new MyNode(val, m_head->next);
        m_head->next = pAdd;
        m_length++;
    }
    
    void addAtTail(int val) {
        MyNode* pAdd = new MyNode(val, nullptr);
        MyNode* pNow = m_head;
        while(pNow->next) {
            pNow = pNow->next;
        } pNow->next = pAdd;
        m_length++;
    }

    void addAtIndex(int index, int val) {
        if(index > m_length) { return; }

        MyNode* pNow = m_head;
        while(index--) {
            pNow = pNow->next;
        }

        MyNode* pAdd = new MyNode(val, pNow->next);   
        pNow->next = pAdd;
        m_length++;
    }

    void deleteAtIndex(int index) {
        if(index >= m_length) { return; }

        MyNode* pNow = m_head;
        while(index--) {
            pNow = pNow->next;
        }

        MyNode* pDel = pNow->next;
        pNow->next = pDel->next;
        pDel->next = nullptr;
        delete pDel;
        m_length--;
    }
private:
    MyNode* m_head = nullptr;
    int m_length = 0;
};

# 3、206. 反转链表

容易想到，双指针一次遍历即可：

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode* pPre = nullptr;
        ListNode* pNow = head;
        while(pNow) {
            ListNode* pNext = pNow->next;
            pNow->next = pPre;
            pPre = pNow;
            pNow = pNext;
        } return pPre;
    }
};

递归版本比较抽象，忽略下面的注释，这样思考就行了：
先看倒数第二第三句，其作用是把当前节点的前后节点进行翻转，当前节点为传入参数 pNow。
再回过头看第二行，把下一个节点递归传入本函数，得到一个 tail，而层层递归之后，这里的 tail 一定会得到链表的结尾，也就是第一行的 nullptr。而每一次递归把 pNow 的下一个节点传入，传入之后在倒数第二三行都会对该节点的前后节点进行翻转。

class Solution {
public:
    ListNode* reverseList(ListNode* pNow) {
        //当递归到最底层找到尾节点之后开始返回 pNow此时指向尾节点
        if(pNow == nullptr || pNow->next == nullptr) { return pNow; }
        //这里的tail就是最后一个节点;每次递归往后探索直到上面条件满足，指向尾节点并返回
        ListNode* tail = reverseList(pNow->next);
        //如果链表是 1->2->3->4->5，那么此时的tail就是5
        //在倒数第二层，pNow->next进入最底层递归满足(pNow->next)->next为nullptr，说明此时pNow为4
        //即pNow是4，pNow的下一个是5，下下一个是空
        //所以pNow->next->next = pNow 就是5往回指向4
        pNow->next->next = pNow;  //pNow->next->next在最底层为nullptr，转而往回逆转
        //后面递归的每一次返回时，pNow所指向的都是待逆转的前一个节点，而返回的始终是尾指针
        //防止链表循环，需要将pNow->next设置为空
        pNow->next = nullptr;
        //每层递归函数都返回tail，也就是最后一个节点
        return tail;
    }
};

# 4、24. 两两交换链表中的节点

一开始想出来的方法需要用到 pre、cur、next 三个指针：

class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        if(head == nullptr || head->next == nullptr) return head;
        ListNode* dummy = new ListNode(-1, head);
        ListNode* pre = dummy;
        ListNode* cur = head;
        ListNode* next = cur->next;
        while(cur != nullptr && next != nullptr) {
            pre->next = next;
            cur->next = next->next;
            next->next = cur;
            pre = cur;
            cur = cur->next;
            if(cur) {
                next = cur->next;
            }
        } return dummy->next;
    }
}

但实际上两个指针就足够了：
思路就是模拟。

class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        if(!head || !head->next) return head;
        ListNode dummy = ListNode(555);
        ListNode* next = head->next;
        ListNode* last = &dummy;

        while(head && head->next) {
            next = head->next;

            head->next = next->next;
            next->next = head;
            last->next = next;
            last = head;

            head = head->next;
        } return dummy.next;
    }
}

递归版本，同样地很抽象：
同样地，理解思路参考上面反转链表那道题的递归解法：
先看倒数第二行，将 next 节点指向 head。再看倒数第三行，将 head 节点指向 “下一坨” 链表。
对于每一个 swapPairs 函数，传入一个 head，处理 head 和 next 两个节点，然后把 next->next 作为新的 head 传入。
函数第一行则是处理最终情况。

class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        if(!head || !head->next) return head;

        ListNode* nextNode = head->next;
        head->next = swapPairs(nextNode->next);
        nextNode->next = head;
        return nextNode;
    }
}

# 5、19. 删除链表的倒数第 N 个结点

#双指针 #快慢指针

可能是因为以前做过好几次了吧，看到题目死去的记忆就开始浮现出来了。
这道题最常规的做法当然是，两次遍历，第一次求得链表长度，第二次遍历则步进 size - n 次，得到倒数第 N 个结点的位置。但其实有更好的做法，一次遍历足矣。那就是双指针！（也可以说是快慢指针啦）

快慢指针均从链表头开始，快指针先走 n 步，然后快慢指针同时开始向后遍历，直到快指针遍历到链表尾部。
此时，由于我们快慢指针之间的距离固定为 n，故慢指针所指向的位置就是倒数第 n 个结点。

class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* slow = head;
        ListNode* fast = head;
        while(n--) {
            fast = fast->next;
        }

        if(!fast) {  // 由于我们没有 dummy 结点，所以多了额外的边界条件处理逻辑
            ListNode* ret = head->next;
            delete head;
            return ret;
        }

        while(fast->next) {  // 如果是 while(fast)，则退出循环时 slow 指向倒数第 N 个元素
            slow = slow->next;
            fast = fast->next;
        }  // 此时我们的 slow 指向倒数第 N 个元素的上一个元素
        
        ListNode* del = slow->next;
        slow->next = del->next;
        delete del;
        return head;
    }
};

这里如果加上 dummy 结点会更简洁一点：

class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* dummyHead = new ListNode(-1, head);
        ListNode* pFast = dummyHead;
        ListNode* pSlow = dummyHead;

        while (n--) { pFast = pFast->next; }

        while (pFast->next) {
            pFast = pFast->next;
            pSlow = pSlow->next;
        }

        ListNode* pDel = pSlow->next;
        pSlow->next = pDel->next;
        delete pDel;
        return dummyHead->next;
    }
};

# 6、面试题 02.07. 链表相交

#双指针 #快慢指针 #哈希

思路 1：
其实我最先想出来的思路是这个，但是没做出来...
很简单的思路，两个指针分别指向 A 和 B，然后同时向后迭代。
A 指针遇到 A 链表尾后，重新指向 B 链表。
B 指针遇到 B 链表尾后，重新指向 A 链表。
那么，如果两个链表相交，则 A 和 B 两个指针一定会相遇。

理由是：
假设两个链表相交与 x 点，公共部分长度为 c，A 链表多出来的部分长度为 a，B 链表多出来的部分为 b。
显然有： a + c + b = b + c + a ，而该公式的物理含义（可以画图看看），就是 A 指针走完 A 链表，又从 B 链表走到交叉点，同时 B 指针走完 B 链表，又从 A 链表走到交叉点。此时，指针相遇。
而对于不相交的情况，同样会有 m + n = n + m 成立，此时两指针均位于链表尾，下一次迭代时两个指针均为 nullptr ；

class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        if(headA == nullptr || headB == nullptr) {
            return nullptr;
        }

        ListNode *pA = headA, *pB = headB;
        while(pA != pB) {
            pA = (pA == nullptr ? headB : pA->next);
            pB = (pB == nullptr ? headA : pB->next);
        } return pA;
    }
};

思路 2：
先对齐，再向后同时步进。
先各自求出两个链表的长度，以及二者的长度差 n。
然后长的链表先走 n 步，此时可以视作长短链表对齐。这时再同时向后遍历，在走完短链表之前，如果指针相等，即相遇。

class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        ListNode* ret = nullptr;
        ListNode* pDummyNodeA = new ListNode(-1, headA);
        ListNode* pDummyNodeB = new ListNode(-1, headB);
        int lengthA = 0, lengthB = 0;

        for(ListNode* pNow = pDummyNodeA; pNow->next != nullptr; pNow = pNow->next) {
            ++lengthA;
        }

        for(ListNode* pNow = pDummyNodeB; pNow->next != nullptr; pNow = pNow->next) {
            ++lengthB;
        }

        int gap = 0, distance = 0;
        ListNode* pNowLong = nullptr, *pNowShort = nullptr;
        if(lengthA > lengthB) {
            gap = lengthA - lengthB;
            distance = lengthB;
            pNowLong = pDummyNodeA->next;
            pNowShort = pDummyNodeB->next;
        } else {
            gap = lengthB - lengthA;
            distance = lengthA;
            pNowLong = pDummyNodeB->next;
            pNowShort = pDummyNodeA->next;
        }

        while(gap--) { pNowLong = pNowLong->next; }
        for( ; distance--; pNowLong = pNowLong->next, pNowShort = pNowShort->next) {
            if(pNowLong == pNowShort) { // 注意这里不是val相等，需要指针相等
                ret = pNowShort;
                break;
            }
        } return ret;
    }
};

思路 3：
还有一种思路就是，相交的本质其实就是指向同一个结点，既然是同一个结点，那我只要用哈希来判断是否遇到相同结点即可。

class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        unordered_set<ListNode *> visited;
        ListNode *temp = headA;
        while(temp != nullptr) {
            visited.insert(temp);
            temp = temp->next;
        }
        temp = headB;
        while(temp != nullptr) {
            if(visited.count(temp)) {
                return temp;
            }
            temp = temp->next;
        } return nullptr;
    }
};

思路 4：
评论区还有一种取巧的思路，也挺有意思的：
由于题目限定了结点的 val 值为非负数，那么我们先遍历链表 A，把所有值设为某个负值（比如 -41），然后再遍历链表 B，如果发现有负值，那么一定就是相交了。

挺巧妙的。

# 7、142. 环形链表 II

#哈希 #快慢指针

思路 1：
一看到题目想到的思路不是指针，而是哈希。我只要从头开始向后遍历链表，每遇到一个结点就存储，如果遇到的是已经存在于 set 中的，说明遇到环了。如果遇到 nullptr，说明无环，走到尽头了。简洁明了。

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        unordered_set<ListNode*> visited;
        while(head) {
            if(visited.count(head)) {
                return head;
            } else {
                visited.insert(head);
                head = head->next;
            }
        } return nullptr;
    }
};

思路 2：
使用快慢指针，这个思路比较绕比较难想到，and 涉及一些简单的公式计算。

对于这个思路，我们需要确认两个问题：是否有环，以及（在有环的情况下）入环点在哪。

定义快慢两个指针，均从头开始向后遍历，慢指针每次走一步，快指针每次走两步。当快指针不为空时，持续迭代。
如果链表存在环，则快慢指针一定会在环中相遇。
理由很简单，如果快指针为空，则无环。如果快指针不为空，那么终究快慢指针都会入环，而快指针每次比慢指针快一步，可以看作快指针追赶慢指针，他们之间距离越来越短。一定会在环中相遇。

（且一定会在慢指针第一圈走不完的时候就会和快指针相遇。虽然这个信息没啥卵用。）

接下来是确定入环点：
假设链表如图所示。设链表中环外部分的长度为 a。slow 指针进入环后，又走了 b 的距离与 fast 相遇。此时，fast 指针已经走完了环的 n 圈，因此它走过的总距离为 a + n(b+c) + b = a + (n+1)b + nc 。

又因为我们的快指针的速度是慢指针的两倍，所以有等量关系：
a + (n+1)b + nc = 2(a+b) ⟹ a = c + (n−1)(b+c)

这里，a 是我们要求的入环点的位置 / 距离，于是有：从相遇点到入环点的距离（c）加上 n−1 圈的环长（ (n−1)(b+c) ），恰好等于从链表头部到入环点的距离。

于是，当我们找到相遇点时，我们再额外使用一个指针 ptr。起始，它指向链表头部；随后，它和 slow 每次向后移动一个位置。一旦他们相遇，那就是入环点。

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        if(!head) return nullptr;
        ListNode* slow = head;
        ListNode* fast = head;
        while(fast) {
            if(!fast->next) return nullptr;
            slow = slow->next;
            fast = fast->next->next;
            if(fast == slow) {
                ListNode* ptr = head;
                while(ptr != slow) {
                    ptr = ptr->next;
                    slow = slow->next;
                } return ptr;
            }
        } return nullptr;
    }
};

一些没用的讯息：

// 为何慢指针第一圈走不完一定会和快指针相遇： 
// 第一步，快指针先进入环
// 第二步：当慢指针刚到达环的入口时，快指针此时在环中的某个位置(也可能此时相遇)
// 第三步：设此时快指针和慢指针距离为x，若在第二步相遇，则x = 0
// 第四步：设环的周长为n，那么看成快指针追赶慢指针，需要追赶n-x
// 第五步：快指针每次都追赶慢指针1个单位，设慢指针速度1/s，快指针2/s，那么追赶需要(n-x)s
// 第六步：在n-x秒内，慢指针走了n-x单位，因为x>=0，则慢指针走的路程小于等于n，即走不完一圈就和快指针相遇

双指针快慢指针哈希